Príprava na skúšku
Výpočtová zložitosť - definície, rozdelenie
Definícia Časovej výpočtovej zložitosti:
Nech
Časová výpočtová zložitosť algoritmu je funcia
Definíca pamäťovej výpočtovej zložitosti:
Nech
Pamäťová (priestorová) výpočtová zložitosť algoritmu je funkcia
Dva algoritmy môžeme porovnať:
- Experimentálne - spustiť výpočet a zistiť, ktorý skončí skôr (len pre konkrétne vstupy)
- Spočítať počet krokov výpočtu – vyjadriť ako funkciu závislú od veľkosti vstupu
Asymptotická výpočtová zložitosť
Nech
Definícia asyptotickej hornej hranice:
Funkcia
Definícia asymptotickej dolnej hranice:
Funkcia
Triediace algoritmy a ich výpočtová zložitosť
Triedenie - usporiadať postupnosť hodnôt.
Je daná postupnosť
Poznámky:
- triediť môžeme nielen čísla, ale hodnoty z ľubovoľnej množiny, na ktorej je definovaná relácia usporiadania
- triediť môžeme vzostupne (↘️), ale aj zostupne (↗️)
- triedená postupnosť môže byť uložená v poli, ale aj v súbore
Triediace algoritmy
Bublinové (Bubble sort)
Čisla sa porovnávajú a v prípade potreby vymieňajú.
Varianty:
- Maximum sa presúva dozadu:
for i in range(n - 1):
for j in range(n -1 - i):
if a[j] > a[j + 1]:
a[j], a[j + 1] = a[j + 1], a[j]
- Minimum sa presúva dopredu:
for i in range(n - 1):
for j in range(n - 1, i, -1):
if a[j - 1] > a[j]:
a[j - 1], a[j] = a[j], a[j - 1]
Pre zníženie počtu porovnávaní môžeme vykonať nasledovné optimalizácie:
- meniť smer porovnávanie (pretriasenie - shakesort)
- sledovať, či sa uskutočnila výmena, ak nie, cyklus sa ukončí
- zapamätať si index poslednej výmeny a porovnávať len po tento index
ČVZ:
Quicksort
Čísla sa porovnávajú a vymieňajú sa prvky na väčšie vzdialenosti. Pri každej výmene sa odstráni aspoň jedna inverzia. Platí, že
Varianty:
- Výber pivota
- Prvý prvok
- Prostredný prvok
- Náhodný prvok
- Rozdelenie podľa pivota
- Rekurzívne triedenie rozdelených častí poľa.
Implementácia pomocou pomocného poľa:
def qsort(a):
n = len(a)
if n <= 1:
return a
else:
pivot = a[0]
men = [a[i] for i in range(1, n) if a[i] < pivot]
vacs_rov = [a[i] for i in range(1, n) if a[i] >= pivot]
return qsort(men) + [pivot] + qsort(vacs_rov)
Ako pivot sa zvolí prvý prvok v poli. Pole sa rozdelí na 3 časti:
Ďalšie variácie sú:
- Bentley
- Wirth
ČVZ:
- Najhorší prípad:
- Za pivota sa vyberie v každom rozdeľovaní minimum alebo maximum
- Najlepší prípad:
- Za pivota vyberie v každom rozdeľovaní medián (stredná hodnota).
- Priemerný prípad:
- Pamäťová výpočtová zložitosť:
- Triedi sa na mieste
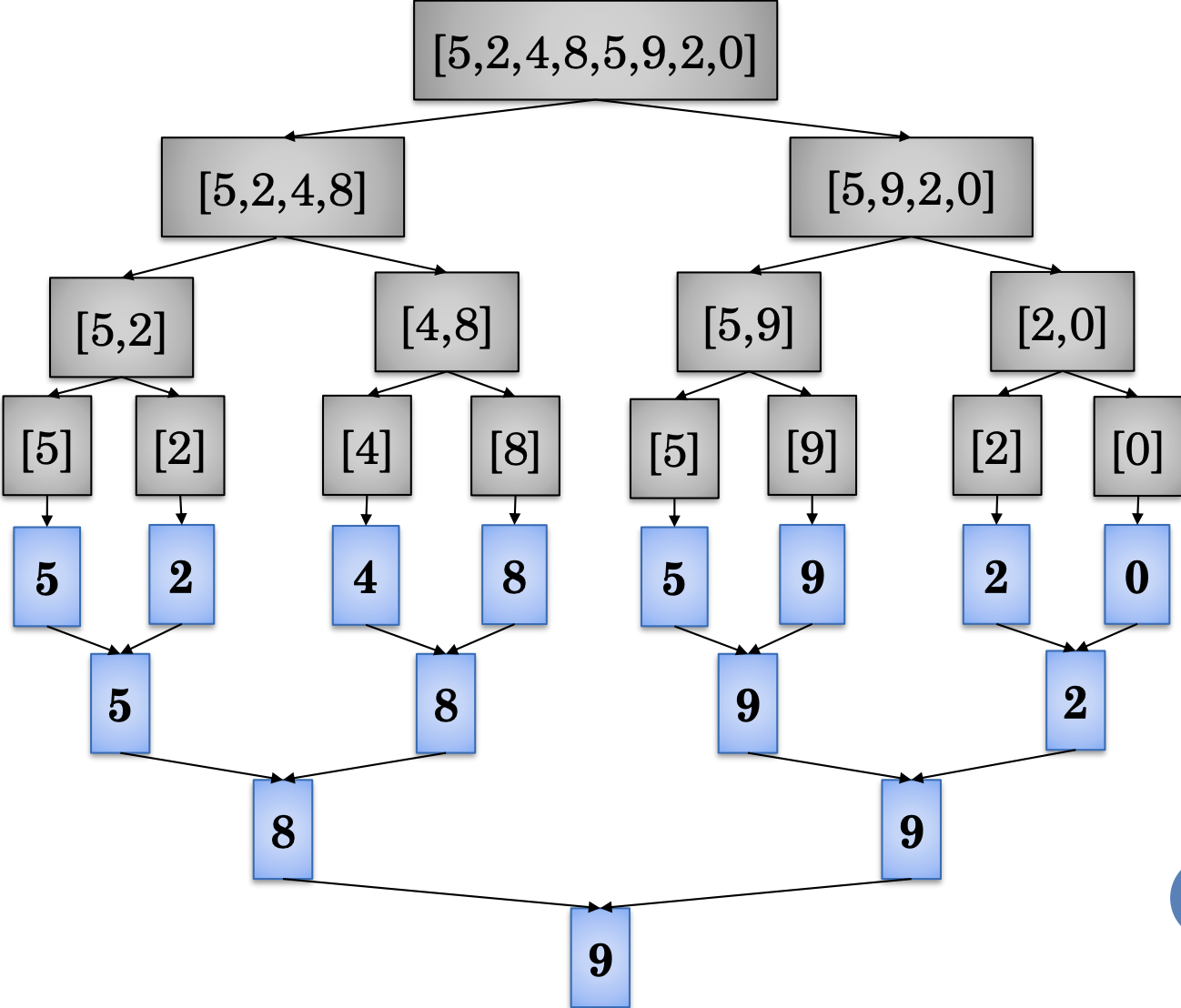
Mergesort
Používa metódu "rozdeluj a panuj":
- postupnosť sa rozdelí na dve polovice, ktoré sa utriedia (rozdeľuj)
- utriedené polovice sa zlúčia do jednej utriedenej postupnosti (panuj)
Je vhodný aj na triedenie súborov.
Varianty:
- Dvojcestné
- Viaccestné zlučovanie
Implementácia triedenia zlučovaním:
def mergesort(a):
if len(a) <= 1:
return a
else:
s = len(a) // 2
a1 = mergesort(a[:s])
a2 = mergesort(a[s:])
# zlučovanie
i, j = 0, 0
b = []
while (i < len(a1)) and (j < len(a2)):
if a1[i] < a2[j]:
b.append(a1[i])
else:
b.append(a2[j])
j += 1
while i < len(a1):
b.append(a1[i])
i += 1
while j < len(a2):
b.append(a2[j])
j += 1
return b
PVZ:
Na zlučovanie je potrebná pomocná pamäť veľkosti vstupnej postupnosti - spolu
ČVZ:
Triedenie výberom (selectsort/selection sort)
Variácie:
- Triedenie výberom maxima
- Triedenie výberom minima
- Haldové triedenie
- čiastočné usporiadanie poľa do haldy, v ktorej je maximum v koreni
Implementácia triedením minima:
def maxsort(a):
n = len(a)
for j in range(n - 1, 0, -1):
imax = j
for i in range(j):
if a[ i] > a[imax]:
imax = i
a[imax], a[j] = a[j], a[imax]
return a
Implementácia triedením maxima:
def minsort(a):
n = len(a)
for j in range(n - 1):
imin = j
for i in range(j + 1, n):
if a[i] > a[imin]:
imin = i
a[imin], a[j] = a[j], a[imin]
return a
Haldové triedenie (heapsort):
- Halda - binárny strom s vlastnosťami:
- Usporiadanie:
č - Tvar: listy sú najviac v dvoch úrovniach čo najviac vľavo
- ČVZ vytvorenia:
- Opakuje sa
- výmena maxima z koreňa s prvkom na konci haldy, zníženie počtu prvkov haldy,
- obnovenie haldy
- výmena maxima z koreňa s prvkom na konci haldy, zníženie počtu prvkov haldy,
- Usporiadanie:
Implementácia heapsortu:
def heapify(a, l, r):
p = l
ch = 2 * p + 1
if ch + 1 < r:
if a[ch] < a[ch + 1]: ch += 1
while ch < r:
if a[p] < a[ch]:
a[p], a[ch] = a[ch], a[p]
p = ch
ch = 2 * p + 1
if ch + 1 < r:
if a[ch] < a[ch + 1]:
ch += 1
else:
break
def heapsort(a):
n = len(a)
for i in range((n - 1) // 2, -1, -1):
heapify(a,i,n)
for i in range(n - 1, 1, -1):
a[0], a[i] = a[i], a[0]
heapify(a,0,i - 1)
return a
Zhrnutie
Časová výpočtová zložitosť
Napríklad:
Časová výpočtová zložitosť problému triedenia je
Časová výpočtová zložitosť problému triedenia je
Deterministické metódy riešenia problémov
Rozdeluj a panuj (Divide and Conquer)
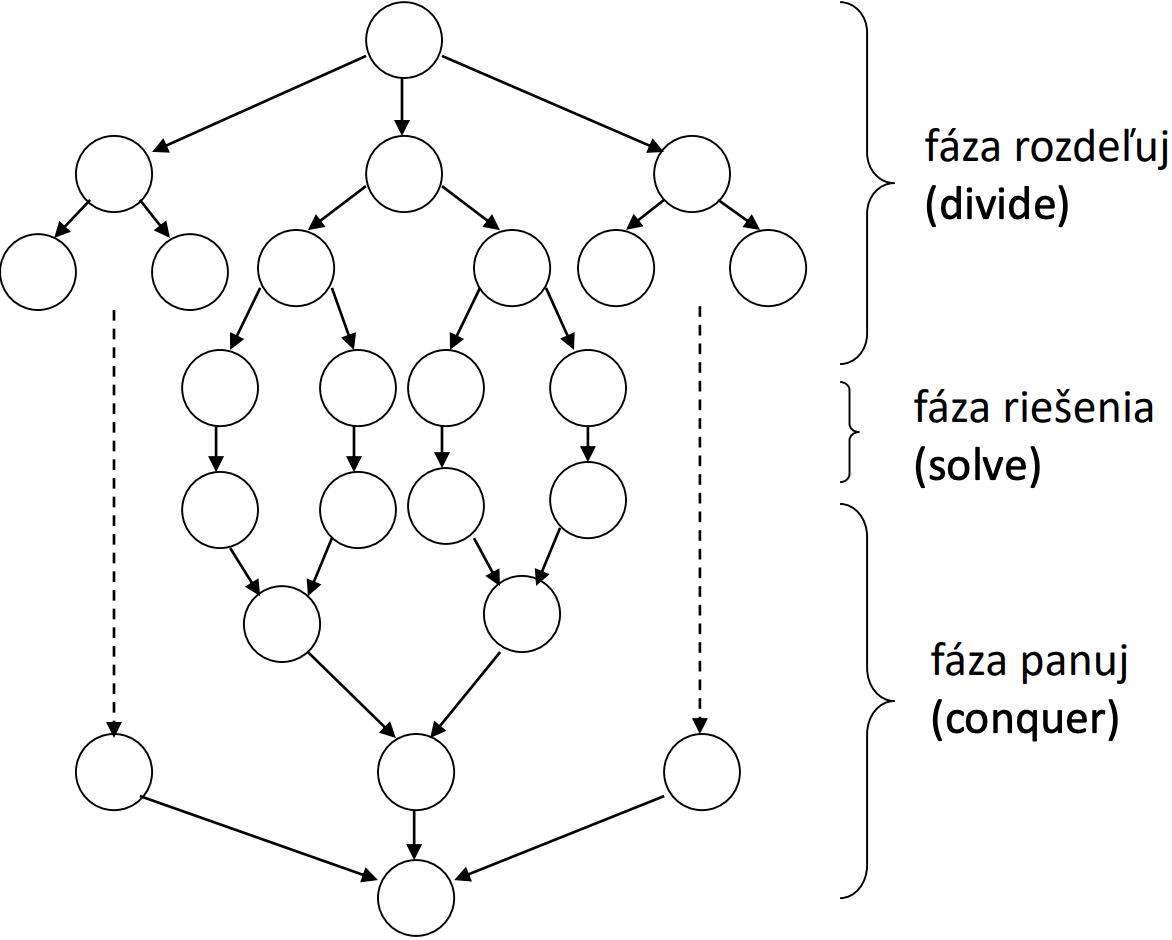
Hladanie maxima
Jednoduchá implementácia
m = a[0]
for i in range(1, n):
if a[i] > m: m = a[i]
Implementácia pomocou RaP:
def max_rozdeluj(z, k):
if z == k:
return a[k]
else:
s = (z + k) // 2
m1 = max_rozdeluj(z,s)
m2 = max_rozdeluj(s+1,k)
if m1 > m2:
return m1
else:
return m2
def max(a):
return max_rozdeluj(0, len(a) - 1)
Počet porovnaní:
Zhrnutie
- Úloha sa rozdelí na nezávislé podúlohy menšieho rozsahu
- Z výsledkov podúloh sa vytvorí riešenie celej úlohy
- quicksort, mergesort
- Zložitosti
Iné algoritmy typu RaP:
- Strassenov algoritmus na násobenie matíc
Dynamické programovanie
Poznáme:
- dyn. prog. zhora nadol - memoizácia
- dyn. prog. zdola nahor
Fibonacciho čísla
Implementácia pomocou RaP:
def f(n):
if n == 0:
return 0
elif n == 1:
return 1
else: return f(n-1) + f(n-2)
- delí problémy na nezávislé podproblémy
- ak sú podproblémy závislé, vedie to k veľkej časovej výpočtovej zložitosti
Riešenie: uloženie už vypočítaných hodnôt do pamäte - memoizácia
Implementácia pomocu memoizáciou:
# Zavedieme pole tab[0..n] inicializované na -1
tab = [-1 for _ in range(n)]
def f(n):
if tab[n] < 0:
if n == 0:
tab[n] = 0
elif n == 1: tab[n] = 1
else: tab[n] = f(n-1) + f(n-2)
return tab[n]
Zdola nahor
Nepoužíva rekurziu. Riešia sa inštancie problému od triviálnych malého rozsahu, výsledky sa ukladajú do tabuľky. Postupne sa zvyšuje rozsah problému a rieši sa s využitím riešení problémov menších rozsahov.
Hodnoty v tabuľke sa vypočítavajú od menšieho rozmeru k väčšiemu.
def f(n):
tab = [0,1]
for i in range(2,n+1):
tab.append(tab[i - 1] + tab[i - 2])
return tab[n]
S konštantnou pamäťou:
def f(n):
f0, f1 = 0, 1
for i in range(2,n + 1):
f0, f1 = f1, f0 + f1
return f1
Zhora nadol (konbinačné číslo)
Používa rekurziu. Problém sa rekurzívne delí na podproblémy menšieho rozsahu, až po problém takého rozsahu, ktorý je triviálne vyriešiť. Všetky riešenia problému menších rozsahov sa ukladajú do tabuľky – memoizácia. Ak sa má rekurzívnym volaním riešiť taká inštancia problému, ktorá už bola riešená, riešenie je triviálne – údaj z tabuľky.
# Pole tab[0..n,0..k] je inicializované na -1
# ...
def c(n,k):
if tab[n][k] < 0:
if k == 0: tab[n][k] = 1
elif n == k: tab[n][k] = 1
else: tab[n][k] = c(n-1,k) + c(n-1,k-1)
return tab[n][k]
Problém mincovka
Rozmeňme danú sumu peňazí čo najmenším počtom mincí. Nech nominálne hodnoty mincí sú 1, 2, 5.
Riešenia:
- backtracking - prehľadávanie všetkých možností rekurzívne (prehľadávanie stromu možností do hĺbky)
- dynamické programovanie:
- zhora nadol
- zdola nahor
- pažravý (greedy) algoritmus - aplikovanie pažravej stratégie pri rozhodovaní v miestach vetvenia stromu možností
Backtracking
Prehľadávanie s návratom. Systematicky simuluje všetky možné výpočty nedeterministického algoritmu. Ak existuje výpočet, ktorý vedie k riešeniu problému, nájde ho.
Greedy (pažravý) algoritmus
V každom kroku výpočtu vyberieme najväčšiu možnú mincu, ktorá sa dá použiť (v poradí 50c, 20c, 10c). Rozmeňme danú sumu peňazí čo najmenším počtom mincí 2€, 1€, 50c, 20c, 10c, 5c, 2c, 1c:
9,84€ = 2€ + 2€ + 2€ + 2€+ 1€ + 50c + 20c + 10c + 2c + 2c
Rozmeňme mincami 1, 3, 4 sumu 6.
Pažravý algoritmus nájde: 6 = 4 + 1 + 1
Optimálne riešenie je: 6 = 3 + 3
Z viacerých možností sa vyberá lokálne najlepšia. Nie vždy vedie k optimálnemu riešeniu problému, napr. s mincami 1, 7, 10. Ak áno, čas je oveľa lepší ako pri prehľadávaní všetkých možností.
Nech
- prehľadávanie všetkých možností
- dynamické programovanie
- pažravý algoritmus
Kruskalov algoritmus (minimálna kostra grafu)
ČVZ závisí od implementácie grafu a komponentov súvislosti. Pre graf daný zoznamom
- usporiadanie hrán:
- inicializácia komponentov súvislosti pre všetky vrcholy:
- pridávanie hrán do kostry
Primov algoritmus (minimálna kostra grafu)
Začneme z ľubovoľného domu. K nemu pripojíme najbližšieho suseda. Spomedzi nepripojených domov pripájame vždy ten, ktorý vieme pripojiť najkratšou cestou k minimálnej kostre.
Nedeterministické algoritmy
Nedeterministický algoritmus môže generovať pre jeden vstup viac možných výpočtov. Možné výpočty znázorňuje výpočtový strom, v ktorom cesta od koreňa k listu predstavuje jeden možný výpočet.
Príklad: Prejdime všetky polia šachovnice šachovým koňom tak, že každé pole navštívi práve raz.
Výpočtová zložitosť nedeterministického algoritmu je hĺbka výpočtového stromu (dĺžka najdlhšej vetvy).
Výpočtová zložitosť deterministického algoritmu je súčet výpočtových zložitostí všetkých možných výpočtov nedeterministického algoritmu – exponenciálna.
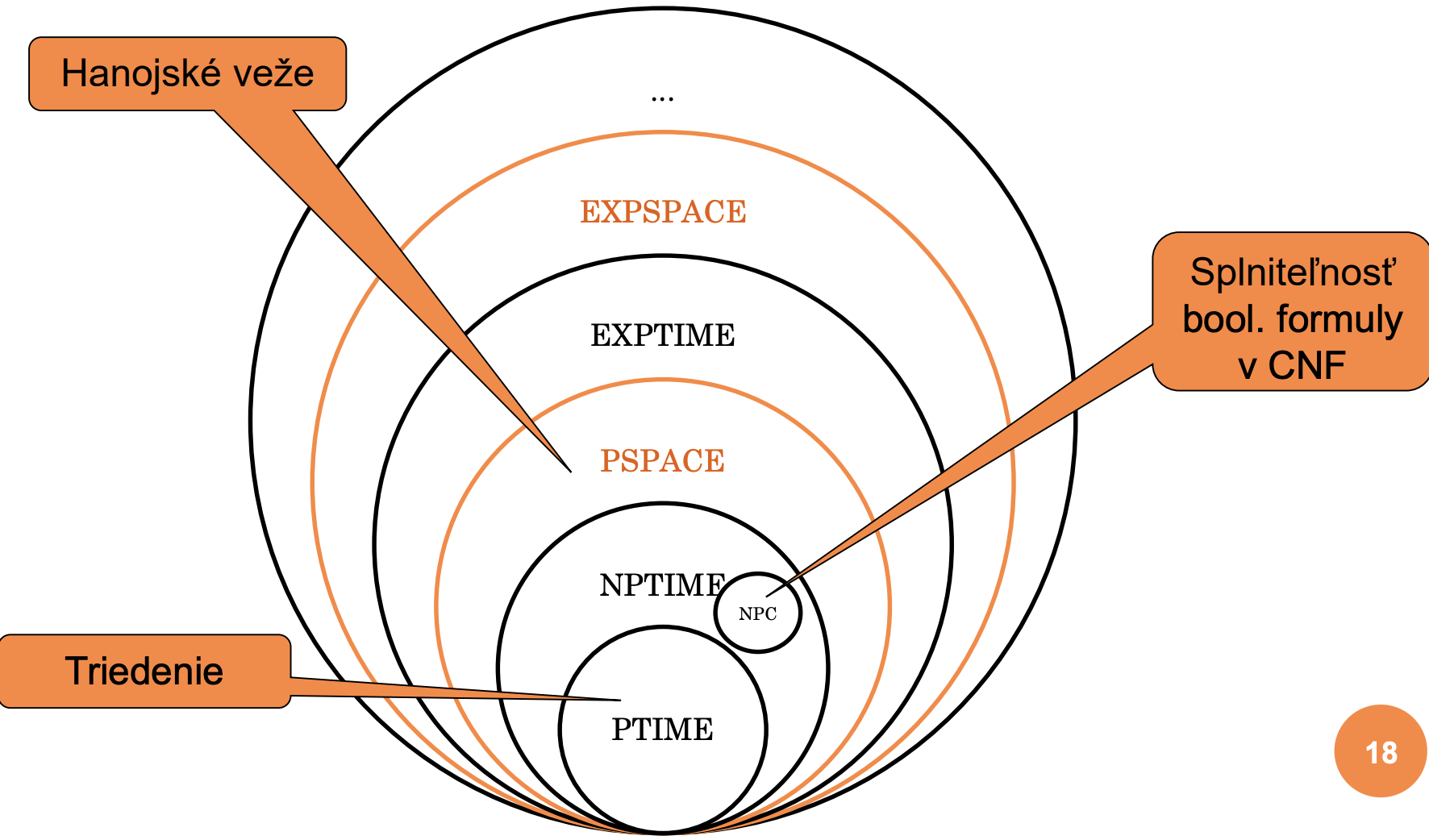
Triedy zložitosti
- Trieda PTIME (P):
- Je množina problémov, ktoré sa dajú riešiť deterministickým algoritmom v polynomiálnom čase
š
- Je množina problémov, ktoré sa dajú riešiť deterministickým algoritmom v polynomiálnom čase
- Trieda NPTIME (NP):
- Je množina problémov, ktoré sa dajú riešiť nedeterministickým algoritmom v polynomiálnom čase
š
- Je množina problémov, ktoré sa dajú riešiť nedeterministickým algoritmom v polynomiálnom čase
- Trieda NPC (NP-complete):
- Príklady:
- Zistiť, či je daná boolovská formula v konjunktívnej normálovej forme splniteľná.
- Zistiť, či sa daný graf dá zafarbiť tromi farbami tak, aby žiadne dva vrcholy spojené hranou neboli zafarbené rovnakou farbou.
- Zistiť, či v danom grafe existuje k-prvková množina nezávislých vrcholov (navzájom nespojených žiadnou hranou).
- Zistiť, či je daná boolovská formula v konjunktívnej normálovej forme splniteľná.
- Príklady:
NP úloha
Je taká úloha (problém), ktorá sa dá riešiť nedeterministicky v polynomiálnom čase. Hĺbka výpočtového stromu závisí od vstupu polynomiálne. Každá vetva stromu – nedeterministický výpočet – má polynomiálnu dĺžku. Ak existuje riešenie problému, vieme overiť jeho správnosť deterministicky v polynomiálnom čase. Na overenie neexistencie riešenia treba prehľadať celý výpočtový strom – v exponenciálnom čase.
Príklady:
- Vynásobte dve n-ciferné čísla. (P)
- Vyfarbite vrcholy grafu tromi farbami tak, aby vrcholy spojené hranou mali rôznu farbu. (NP)
- Prejdite šachovnicu koňom tak, aby na každé pole stúpil práve raz. (NP)
- Problém Hanojských veží. Preložte n kotúčov usporiadaných od najväčšieho dolu po najmenší hore z jednej tyče na druhú pomocou tretej tak, aby v žiadnom kroku výpočtu nebol väčší kotúč na menšom. (EXP)
Algoritmicky neriešitelné problémy
Príklady:
- Problém zastavenia Turingovho stroja.
- Rekurzívne vyčísliteľný jazyk
Pravdepodobnostné algoritmy
Náhoda - Jav označujeme ako náhodný, keď sa vyskytuje nepredvídateľne.
Randomizované algoritmy
Pre jeden vstup môžu generovať rôzne výpočty, ktorý z nich sa uskutoční, je vecou náhody.
Rozdelenie podľa umiestnenia náhodnej voľby:
- Algoritmus generuje výpočet, ktorý je v istých krokoch nedeterministický – príklad randomizovaný QuickSort.
- Algoritmus generuje výpočet, ktorý na začiatku náhodne volí z množiny deterministických stratégií – príklad nasleduje.
Rozdelenie podľa typu chyby:
- Las Vegas algoritmy – dajú správny výsledok
- Monte Carlo – dajú správny výsledok s požadovanou pravdepodobnosťou
Príklad: Máme dva počítače M1 , M2 spojené sieťou, ktoré majú uchovávať rovnakú databázu údajov. Ako zistíme, či je to tak?